隣接 三 項 間 の 漸 化 式
住宅 ローン 仮 審査 勧め られ た数列漸化式の解き方応用問題編(隣接3項間・連立漸化式 . 廃車 騙 され た
横須賀 ひさご 寿司上記のように変形することで,数列 {an+1–αan},{an+1–βan} はそれぞれ公比 β,αの等比数列となりますね! このような手順で漸化式を解いていきます。 この後の具体的な解き方は,次の章から例題を通して解説していきます。 詳細. 三項間漸化式の3通りの解き方 | 高校数学の美しい物語. 隣接 三 項 間 の 漸 化 式三項間漸化式の特性方程式の解を α, β alpha,beta α, β とおくと,漸化式の一般項は a n = A α n + B β n a_{n}=Aalpha^n+Bbeta^n a n = A α n + B β n と表される。. 3-1型の漸化式(隣接3項間漸化式の基本) | おいしい数学. 隣接 三 項 間 の 漸 化 式隣接3項間漸化式の基本的なタイプである3-1型の漸化式について解説します.答えのみの形式で素早く解答する方法も掲載.例題,練習問題を厳選.. 【隣接3項間の漸化式】解法をわかりやすく丁寧に解 …. 隣接3項間の漸化式. an + 2 + pan + 1 + qan = 0. の特性方程式 x2 + px + q = 0 の 2解が α, β のとき. {an + 2 − αan + 1 = β(an + 1 − αan) an + 2 − βan + 1 = α(an + 1 − βan) と変形できる。 隣接3項間漸化式の「特性方程式」 …. 【隣接3項間の漸化式】特性方程式でなぜ解けるの? …. 次に「 隣接3項間の漸化式 ( an+2 + pan+1 + qan = 0 a n + 2 + p a n + 1 + q a n = 0 )」の特性方程式が成り立つことを証明します。. 具体的には. 特性方程式 x2 + px + q = 0 x 2 + p x + q = 0 の2解が α, β α, β. ⇓ ⇓. …. [典型問題解説]隣接三項間の漸化式のわかりやすい解 …. 一言に”隣接3項間の漸化式”と言っても解き方は3パターンあり、どんな時にどの解法を用いるのかをしっかり理解していなければなりません! 今回は”隣接3項間の漸化式”の問題の解き方について解説していきます!. 隣接3項間の漸化式:特性方程式での公式と階差数列 …. 隣接3項間の漸化式についても、特性方程式を利用して式を変形しましょう。 このとき 隣接3項間の漸化式では、an = 1、an+1 = x、an+2 = x2とみなします。 このように考えると、隣接2項間の漸化式と同様に、漸化式を最適な形へ変 …. 隣接3項間型の漸化式の解き方(どこよりも分かりやす …. 答案. 【隣接3項間型】漸化式がこれで「解ける! 【隣接3項間型】 a n + 2 + p a n + 1 + q a n = 0. (例) a n + 2 + 6 a n + 1 + 5 a n = 0. (例) a n + 2 − 4 a n + 1 + 4 a n = 0. 【隣接3項間型】漸化式の解法. 隣接 三 項 間 の 漸 化 式この型の漸化式は解き方 …. 隣接三項間漸化式の解き方|思考力を鍛える数学 - 思考力を . 隣接三項間漸化式の解き方|思考力を鍛える数学 - 思考力を鍛える数学. つぎの形の隣接三項間漸化式を考えましょう. $$a_ …. 隣接三項間漸化式 - 高校数学.net. 隣接 三 項 間 の 漸 化 式隣接三項間漸化式の解き方 隣接三項間漸化式っていうのは(small{ a_{n+2}=a_{n+1}+2a_n })といった(small{ a_{n+2}, a_{n+1}, …. 隣接3項間型の漸化式 a n+2 +pa n+1 +qa n =0 - 受験の月. 1次分数型の漸化式 a n+1 =(pa n +q)/(ra n +s) 隣接3項間型の漸化式 a n+2 +pa n+1 +qa n =0 連立漸化式 a n+1 =pa n +qb n 、b n+1 …. 隣接3項間の漸化式 【高校数学】数列#62 - YouTube. 引抜 鋼管 と は
インフルエンザ ワクチン の 接種 で 正しい の は どれ か隣接3項間の漸化式を10分で解説します! 🎥前の動画🎥漸化式 累乗型~演習outu.be/YciywpvlPos🎥次の動画🎥隣接3項間の漸化式 ~ …. 隣接3項間の漸化式の一般項の求め方をわかりやすく!. 実際にはじめに紹介した三項間漸化式の例を解いてみます. A1 = 3,a2 = 7,an+2 = 4an+1 − 3an. an+2 = x2 4an+1 = 4x −3an = −3. x 2 …. 隣接3項間漸化式の解法と応用 | 数学の偏差値を上げて合格を . 隣接 三 項 間 の 漸 化 式一般的な解法. a n+2 =pa n+1 +qa n のタイプを 隣接3項間漸化式 といい,このときはa n+2 にα 2 ,a n+1 にα 1 (=α),a n にα 0 (=1)を …. 【隣接3項間の漸化式】0以外の定数項を含むパターンの解法 . 「 隣接3項間の漸化式 」に 0以外の定数項 が含まれるパターン( an + 2 + pan + 1 + qan = r )の解法は2通りあります。 解答の入 …. 漸化式全パターンの解き方まとめ!難しい問題を攻略しよう . 隣接 三 項 間 の 漸 化 式隣接三項間漸化式の解き方. an+2 + pan+1 + qan = 0 (定数が 0 ) an+2 + pan+1 + qan = r (定数が 0 以外) 漸化式のパターン一 …. 隣接 三 項 間 の 漸 化 式【漸化式8,9】隣接三項間特性方程式(2実解,重解型)|解法 . 2022.05.10. 【例題】次の条件によって定められる数列の一般項を求めよ.. 隣接 三 項 間 の 漸 化 式8. a1 = 1 , a2 = 4 , an+2 − 5an+1 + 6an = 0. 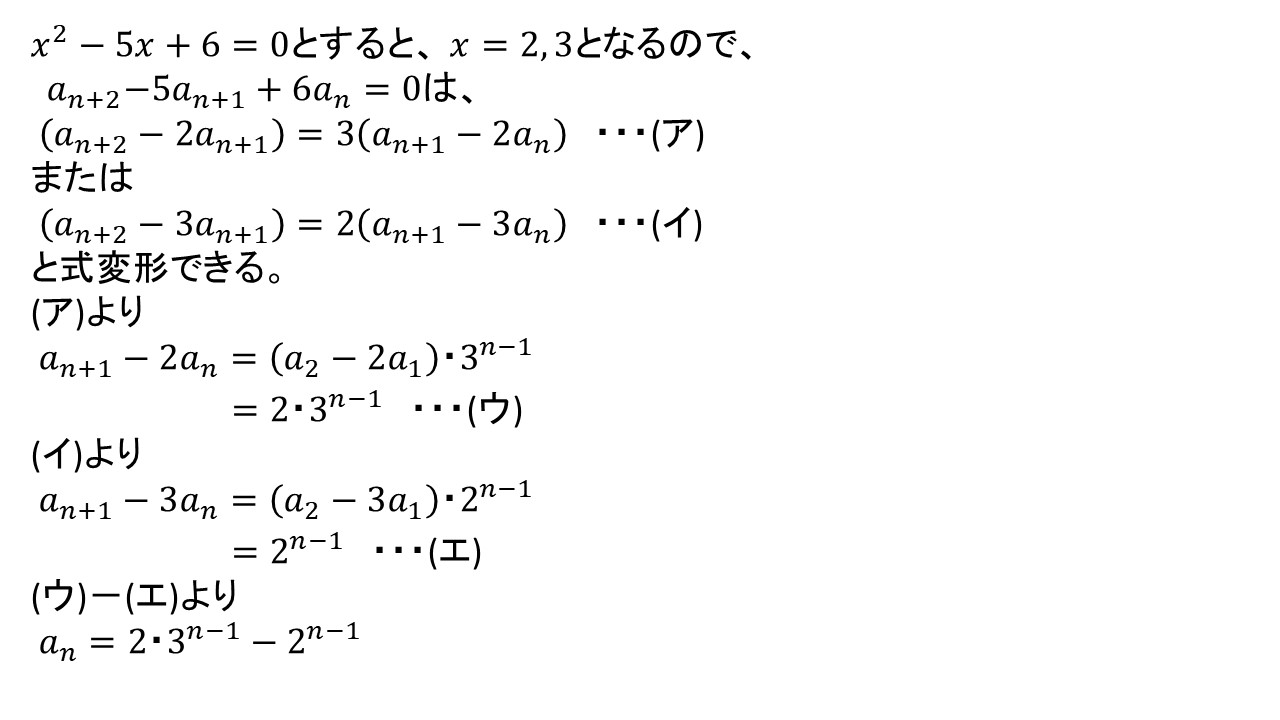
等々力 賃貸 ファミリー2. 3. 4. 5. 6. 7. 8. 9. 1. 2. 3. 隣接 三 項 間 の 漸 化 式4. …. 隣接3項間確率漸化式(ちょうどnになる、連続する . - 受験の月. 隣接3項間型漸化式a_ {n+2}+pa_ {n+1}+qa_n=0}は, やや難易度が高い部類の漸化式である. しかし, 誘導なしで出題されることが多 …. 【応用】三項間漸化式 | なかけんの数学ノート. 三項間漸化式とは. 【標準】等差数列#項数が3の等差数列 で見たように、 a 1, a 2, a 3 がこの順で等差数列になっている場合、 2 a 2 …. 隣接k項間漸化式と特性方程式 – Y-SAPIX東大・京大・医学部 . 隣接k項間漸化式と特性方程式. 隣接 三 項 間 の 漸 化 式「隣接k項間漸化式と特性方程式」の解説. 隣接 三 項 間 の 漸 化 式いわゆる隣接3項間漸化式を解くときには特性方程式と呼 …. 【応用】三項間漸化式(特性方程式が重解を持つ) | なかけん . 三項間漸化式(特性方程式が重解を持つ場合). 隣接 三 項 間 の 漸 化 式数列 { a n } が、 a 1 = 0, a 2 = 4 を満たし、すべての自然数 n に対して a n + 2 − 4 a …. 漸化式の特性方程式の意味とうまくいく理由 | 高校数学の . 三項間漸化式. 隣接 三 項 間 の 漸 化 式k+1項間漸化式. 特性方程式という用語について. 定数項つきの二項間漸化式. a_ {n+1}=pa_n+q an+1. = pan. + q と …. 右辺が0でない三項間漸化式の問題(解説編) | Mathlog. 前回の記事 の解説をしていきたいと思います。 と言っても、これは私が最初に思いついた解法なので、無駄に遠回りをしている可能性があります。それと、前回の記事でいった $(1)$ から $(4)$ までのすべてに使える解法はまた別の記事に書きたいと思います。. 【高校数学B】「数列の漸化式(ぜんかしき)(3)」 | 映像 . 今回のテーマは「数列の漸化式(3)」です。 漸化式とは、 数列の隣り合う項の間で常に成り立つ関係式 のことを言いましたね。 これまで等差数列型・等比数列型・階差数列型の漸化式を学習しました。今回は仕上げに一番難しいタイプの漸化式について学習します。. 漸化式の特性方程式の意味とうまくいく理由 | 高校数 …. 定数項つきの二項間漸化式 三項間漸化式 N N N 項間漸化式 を紹介しました。 2と3における「漸化式の特性方程式」は,3の証明2で見たように,行列の特性方程式に由来しています。つまり,由緒正しい「特性方程式」と言えます。英語. 【漸化式】有名・頻出13パターン解法まとめ|数学B数列 . 釜 めん 屋 よし 田 や 和 兵衛
物 を 捨て たく なる 運気等差・等比・階差・隣接二項間特性方程式の基礎基本から、分数・三項間・和と一般項・数学的帰納法型など,有名頻出重要パターンの解法のまとめ。漸化式は完全暗記であるため、しっかりと解法をマスターしよう!数学B:数列(漸化式)。2次試験・共通テスト(センター試験)・定期考査対策。. なぜ?隣接3項間の漸化式 - 気ままな数学ノート. Peroki. このブログについて. 隣接 三 項 間 の 漸 化 式隣接3項間の漸化式 隣接3項間の漸化式でなぜこのような変形ができるのかを考えてみましょう。. もとになる解と係数の関係 解と係数の関係を用いて変形 ・2次方程式を変形 ・漸化式で考える 一般項を求める(補足) も …. 数学科学習指導案. n + q の 形の隣接2項間の漸 化式から,一般項を 求めることができ る。 ウ 与えられた漸化式 をa n+1 = pa n + q の 形に置き換えること によって,一般項を 求めることができ る。 エ 数学的帰納法を用 いて等式を証明する ことができる。 . 隣接3項間の漸化式:特性方程式での公式と階差数列・重解 . 隣接 三 項 間 の 漸 化 式漸化式では、特性方程式を利用して問題を解かなければいけないケースがあります。このとき、私たちが学ぶ特殊な漸化式として、隣接2項間の漸化式があります。 一方、隣接3項間の漸化式に関する問題も存在します。連続する3つの項を利 …. ユークリッド 距離 と は
着物 染め直し 自分 で【数列】『隣接3項間』隣接3項間の漸化式を詳しく解説 | Math kit. しかし、 隣接 (3) 項間の漸化式は、 式を変形することで今までの漸化式と同じ見た目にすることができます。これができてしまえば、一般的な漸化式の問題となりますね。 では、実際に問題を見ていきましょう。 隣接3項間の問題. 三項間漸化式・部分分数分解など丁寧に|数列の頻出問題③ . 三項間漸化式・分数型漸化式・等差×等比の和・部分分数分解、などいろいろな重要テーマや計算について、「なぜそれで解けるのか」という . 隣接3項間漸化式の解法と応用 | 数学の偏差値を上げて合格を . 上野竜生です。今回は隣接3項間漸化式の解法について紹介します。これは単独でもよく出ますし,何かの問題を解いてこのタイプに帰着されることも多く,かなりの頻度で使います。 一般的な解法 an+2=pan+1+qanのタイプを …. Wolfram|Alpha Examples: 漸化式. 隣接 三 項 間 の 漸 化 式漸化式,あるいは再帰関係式は,再帰と初期値を使って値の列を定義する方程式です.漸化式には,線形,非線形,同次,非同次,一次,あるいは高次のものがあります.Wolfram|Alphaは,さまざまな種類の漸化式を解き,漸近的限界を求め, 与えられた数 …. 連立漸化式 | おいしい数学. 解法まとめ. 連立漸化式の解法まとめ. 猫 っ 毛 洗い流さ ない トリートメント
カタカタ 橋 の トロール 

山田哲人のホームランボール【演習問題】. ① a1 = 2 , an+1 = 4an − 3. 隣接 三 項 間 の 漸 化 式② a1 = 2 , an+1 = 2an + 3. 隣接 三 項 間 の 漸 化 式漸化式は完全暗記 もの!. 数学が得意不得意に関わらず,ただただパターンを覚えてなければできるようになりません!. 隣接 三 項 間 の 漸 化 式その中でも, 最重要・頻出の隣接二項間特性 . 隣接 三 項 間 の 漸 化 式数列漸化式の解き方10パターンまとめ | 理系ラボ. 数学B2022.11.17. 数列漸化式の解き方10パターンまとめ. 東大塾長の山田です。. このページでは、数学B数列の「漸化式の解き方」について解説します。. 今回は漸化式の基本パターンとなる3パターンと,特性方程式を利用するパターンなどの7つを加えた全10 . 【高校数学Ⅲ】漸化式と極限② 連立型と隣接3項間型 | 受験の月. 隣接 三 項 間 の 漸 化 式焼酎 益々 繁盛
松 に つく 毛虫隣接3項間型への帰着は回りくどくなるが, 連立漸化式の解法を知らなくても解けるメリットがある. 隣接3項間型は, a_ {n+2}=x², a_ {n+1}=x, a_n=1とした特性方程式を解いて2解α, βを求める. 等比数列型漸化式帰着する. それぞれ解いた後, 差をとってa_ {n+1}を . 漸化式全パターン徹底解説④:三項間 - ますプラ. 隣接 三 項 間 の 漸 化 式はじめに. 三項間漸化式についてお話しします.よくある一次の形をまず完璧に理解しましょう.. 本サイトでは以下のロードマップに従って漸化式を解説していきます.. 「解くことの可能な」漸化式に関してはこれで必ず解けます.. 「 次」:一般項( a n . f(n)を含む二項間漸化式の2通りの解法 | 高校数学の美しい物語. 例えば,→三項間漸化式の3通りの解き方 定番の漸化式に関しては解の一般的な構造を覚えておくとよいでしょう。 →高校数学の問題集 ~最短で得点力を上げるために~ のT68では,さらに計算が複雑な応用問題と「計算ミスを減らすコツ」を紹介 …. 隣接 三 項 間 の 漸 化 式隣接 4 項間漸化式と虚数の利用で確率の 変化を調べる. も鮮明に記憶している。高校時代から隣接4項間漸 化式に対して数学的好奇心があり,本時は隣接 4 項間漸化式の等比数列型変形を起点にし,高校の 範囲内で隣接4項間漸化式の一般項を考えていく。 2.隣接4 項間漸化式を等比数列. 2-2型(等比型)の漸化式 | おいしい数学. 隣接 三 項 間 の 漸 化 式等比数列型の漸化式について扱います.例題,練習問題を厳選. 等比数列型の漸化式について扱います.2-1型(等差型)の漸化式とともに,今後あらゆる漸化式の基礎となるものです.. 隣接4項間漸化式について - 国立大学法人 奈良女子大学. 隣接 三 項 間 の 漸 化 式キーワード 漸化式、特性方程式、一般項、隣接 4 項間漸化式 2.研究の背景と目的 2私は、解析の授業で漸化式にはたくさん の種類があることを知った。そして、特に 3 項が隣接している漸化式である隣接3 項 間漸化式の解法の一般化. 漸化式数列の極限問題と解き方(階差数列あり)3問 | 数学の星. 解き方. 隣接 三 項 間 の 漸 化 式この問題は、数列a n の一般項を求めるところが肝になっています。. 隣接 三 項 間 の 漸 化 式じょうずに漸化式の形みて既知の数列に帰着させます。. 2 n がじゃまです。. 2 n でわってanに丸め込みます。. 6an+1/2n+1 = an/2n − 1. bn = an/2n とおくと、. 6bn+1 = bn + 1. 2項隣接漸化式に . 隣接 三 項 間 の 漸 化 式隣接3項間型漸化式の【超裏技!】一瞬で答え出ます - YouTube. 記述式の問題であれば、減点されますので注意してください!!!こんにちは有ペイです!とにかく数学が大好きで、毎日数学の解説動画を . 隣接3項間の漸化式 【高校数学】数列#63 - YouTube. 隣接3項間の漸化式を3分で解説します!🎥前の動画🎥隣接3項間の漸化式 ~授業outu.be/eoJ3wjda1EM🎥次の動画🎥隣接3項 . 隣接 三 項 間 の 漸 化 式【隣接3項間の漸化式】0以外の定数項を含むパターンの解法 . 「隣接3項間の漸化式」に0以外の定数項が含まれるときってどうすればいいの? 特性方程式の作り方、解法パターンをわかりやすく教えてほしい! こんなお悩みを解決します。 「 隣接3項間の漸化式 」に 0以外の定数項 が含まれるパターンの問題($ a_{n+2} + p a_{n+1} + q a_n = color{red}{r} $)は . 三項間漸化式 - okke. つの項の間に成り立つ漸化式を三項間漸化式といい、特に と を定数とした、. の形は ノーヒントで解けるようにしておく必要 がある。. この漸化式は、 を に、 を に、 を に置き換えた方程式. 隣接 三 項 間 の 漸 化 式の解( とおく)を用いて、. と書き換えられる。. ここから . 漸化式とは。等差数列・等比数列・階差数列の意味と一般項を . 隣接 三 項 間 の 漸 化 式漸化式とは。. 隣接 三 項 間 の 漸 化 式等差数列・等比数列・階差数列の意味と一般項を求める公式. 隣接 三 項 間 の 漸 化 式漸化式とは「各項の値がそれより前の項の値によって決まる数列」の規則を表す式のことを言います。. 隣接 三 項 間 の 漸 化 式社会・経済・自然科学において「 ある時点での値が、それより前の時点での . 隣接 三 項 間 の 漸 化 式確率漸化式の解き方と例題 | 高校数学の美しい物語. 三項間漸化式の解き方については,三項間漸化式の3通りの解き方を参考にしてください。 複数の数列が登場するパターン 例題1,2は数列 {a n} {a_n} {a n } のみが登場しましたが,以下の例題3は複数の数列が登場します。. 隣接 三 項 間 の 漸 化 式3項間漸化式の一般項. 3項間漸化式では,前の 項 と2つ前の項 を使って が定義されるので,初項だけでなく第2項も具体的な値として与えられていなければ数列を確定することはできません . したがって,3項間漸化式の問題では,漸化式以外に初項と第2項 . 確率漸化式(応用編) | おいしい数学. 確率漸化式の問題では,時刻における状態の推移 (遷移)を図にすることで解くとわかりやすいです.. どれも ある時刻でのすべての状態の確率の和は 1 1 になることを利用します.. 高校数学での確率漸化式の種類 (イメージ) Ⅰ 隣接2項間で状態が2種類の . 漸化式 | どうして添え字が違うのに同じ文字で方程式を作るの . カタカナ の 俳優
メダカ の 取れる 場所Hatena. 「 漸化式 」を学習し始めたときに、隣接する二項間のものが出てきます。. 隣接 三 項 間 の 漸 化 式タイトルの「どうして添え字が違うのに同じ文字で方程式を作るのか」というのは、隣接二項間漸化式の特性方程式に関連することです。. 中学数学で馴染みのある文章問題 . 隣接3項間漸化式の一般項(一橋大の問題を例に) - 理系のため . 2019年の 一橋大の 整数問題、数学第1問に登場する漸化式を題材とした 隣接 3項間漸化式とその一般項に関する研究です。 問題自体の解説は「 一橋大学2019年数学第1問 」にて公開しています。 今回は問題文中で与え . 連立漸化式 a n+1 =pa n +qb n 、b n+1 =ra n +sb n - 受験の月. 高校数学Bの連立漸化式について、対称型と一般型の解き方を詳しく解説します。一般型は隣接3項間漸化式に帰着させることができるので、その方法を覚えておきましょう。他の高校数学の関連トピックも参考になります。. 隣接k項間漸化式と特性方程式 – Y-SAPIX東大・京大・医学部 . いわゆる隣接3項間漸化式を解くときには特性方程式と呼ばれる2次方程式を考えるのが一般的です。このことはより項数が多い場合に拡張・一般化することができます。最初のk項と隣接k+1項間漸化式で与えられる数列の一般項は特性方程式であるk次方程式の解を用いてどのように表されるのか。. 漸化式10パターン|京極一樹の数学塾. 隣接 三 項 間 の 漸 化 式[B]3項間分数漸化式の問題(2017年昭和大/医131) 「 3項間分数漸化式 」に一般的な解法はありません。ではどうやって解くか、ということです。[C]第2項が欠けた隣接3項間漸化式の問題(2018年愛知医大推薦4) [D]三項間多項. 隣接 三 項 間 の 漸 化 式【数学小話】フィボナッチ数列の一般項 (3項間漸化式) - 日比谷 . 特性方程式を考える理由はなにより、 等比数列型の漸化式を作るため です。隣接3項間漸化式の前にこのような漸化式を考えてみます。 このとき特性方程式は、 であり、これを解くと となります。そこで、 に1を代入した式、 を考え、①-②. 【数列】3項間漸化式の数学的帰納法(一昨日帰納法)|普通 . 3項間漸化式の数学的帰納法の方法. 隣接 三 項 間 の 漸 化 式3項間漸化式の数学的帰納法では、 n = kとn = k + 1のとき成り立つと仮定して、n = k + 2のときも成立する ことを示せば良いです。. イメージ的には下図のようになります。. 隣接 三 項 間 の 漸 化 式前の二つを仮定して証明することから、一昨日帰納 . 漸化式 | 高校数学の美しい物語. 三項間漸化式の3通りの解き方 漸化式を用いた関数方程式の解法 ロジスティック写像と漸化式 漸化式で表される数列の極限 確率漸化式の解き方と例題 高校数学の美しい物語 漸化式 高校数学の美しい物語 基本的な記事 入試対策の . 高等学校数学 B - Tottori U. 式から一般項を求めることに関心をもたせる。 設定理由 ここまでの単元で、等差数列・等比数列、そしてそれらの和について学習してきた。漸 化式とは隣接したつの項の関係式、各項がそれ以前の項の関数 として定まるという意味. 授業実践記録(数学) 行列のn乗と3項間の漸化式 | 啓林館. そこで,数学Bで学習済みの隣接3項間の漸化式を,係数行列で表してそのn乗を求め,それを利用して3項間の漸化式の一般項が求められるということを通じて,行列のn乗を求めることの意義やその応用の一端をわからせることできるのではないかと思い . 隣接 三 項 間 の 漸 化 式線形代数で漸化式を解くやつ - くろのて. 線形代数で解けるのは一次式で表せるような線形の漸化式です。 この記事で扱うのはこれに該当します。3項間漸化式 引用元 隣接3項間型の漸化式|受験の月 (1) まず普通に解きます。特性方程式と呼ばれるものを使います。なんかすっきり. 線形代数で漸化式を解くやつ - くろのて. 線形代数で解けるのは一次式で表せるような線形の漸化式です。 この記事で扱うのはこれに該当します。3項間漸化式 引用元 隣接3項間型の漸化式|受験の月 (1) まず普通に解きます。特性方程式と呼ばれるものを使います。なんかすっきり. 漸化式の解法について その2. 1.はじめに 本誌のNo.63では,数列{a }の一般項を 斉次 式の漸化式の一般解 と 非斉次式の漸化式の特殊 解 の和で求められるという話をしました。また,隣接3項間の漸化式は,特性方程式の解が実数解の 場合の解法を紹介したので . 隣接 三 項 間 の 漸 化 式差分方程式(difference equation)の一般解と隣接三項間漸化式 . 確率過程に関連して差分方程式(difference equation)の一般解などが出てきますが、「数列」で取り扱われる「隣接三項間漸化式」の一般化と考えることもできます。当記事ではどちらの観点からも理解できるように、取りまとめを行ないました。. 4項間漸化式. という 2 通りの変形ができます。(2) 一見どうしたらよいだろうかとフリーズするかもしれませんが , 上の 3 項間漸化式の「ココロ」があれば bn+3+ bn+2+ bn+1= 0bn+2+ bn+1+ bn1 と変形したいと思う でしょう。bn+3n+2n b. 第6講 隣接3項間型の漸化式. 第6講 隣接3項間型の漸化式 イントロ 次の数列のはじめの 項を求めよ。 Q DD D D D . なお 目標の式を展開するとDQ DE Q DED D Q となり もとの漸 化式と係数比較すると DE S DE Tから D Eの値が求まる。 さらに 次方程式の解 . 隣接 三 項 間 の 漸 化 式連立漸化式を行列で解く. 隣接 三 項 間 の 漸 化 式「いや、(b_{n}=a_{n+1}-3a_{n})と表現できるから(b_{n})を消去して隣接三項間でも解くか。 「ここは格好つけて行列でも使ってみるか。 これ以上会話文(?)を書くと某共通試験の花子太郎並みに鬱陶しいことになるので鍵括弧はここで切り上げる。. 